Tirage aléatoire dans une loi normale sur plusieurs dimensions
par nojhan le 25 mai 2006
Comment effectuer un tirage aléatoire suivant une loi gaussienne multi-variante (également appelée loi multinormale) ? La réponse et un code C++ en prime.
Une possibilité est de considérer que chaque variable est indépendante des autres. On tire alors chaque variable dans une loi normale, en utilisant la méthode de Box-Muller :
En C++, tirer un chiffre y dans une loi normale de moyenne mean et d’écart-type std, ça donne quelque chose comme :
do {
x1 = 2.0 * randomUniform(0,1) - 1.0;
x2 = 2.0 * randomUniform(0,1) - 1.0;
w = x1 * x1 + x2 * x2;
} while ( w >= 1.0);
w = sqrt( (-2.0 * log( w ) ) / w );
y = x1 * w;
y = (y * std) + mean;
Malheureusement, se contenter de tirer toute les variables indépendamment ne permet pas de représenter une véritable loi multi-variante. Il manque en effet les co-variances.
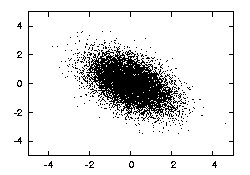
Pour obtenir une loi normale prenant en compte les covariances, il faut déjà définir l’ensemble des variances et des covariances que l’on veut utiliser comme paramètres de la loi. Cela se fait sous la forme d’une matrice de variance-covariance, qui est carrée et symétrique, de la taille du nombre de variables et définie positive.
La première étape consiste à tirer un vecteur (du nombre de variables souhaité) en utilisant pour chaque élément un tirage dans une loi normale centrée réduite. Ensuite, on va factoriser la matrice de variance-covariance par une décomposition de Cholesky. Il suffit alors de pré-multiplier cette matrice par le vecteur aléatoire, et y ajouter un vecteur de moyenne.
En simplifiant, on aurait quelque chose comme ça :
vector< vector<double> > popVarcholesky = cholesky( varcovar );
vector<double> T;
T.reserve(dimension);
for( unsigned int i=0; i<dimension; i++) {
T.push_back( randomNormal( 0.0, 1.0 ) );
}
vector<double> compVar = transpose( matrixMultiply( popVarcholesky, transpose(T) ) );
vector<double> pointFinal;
for( unsigned int i=0; i<dimension; i++) {
pointFinal.push_back( moyennes[i] + compVar[i] );
}
Le code présenté dans l’archive ci-jointe est fait à la va-vite, non optimisé, l’interface est perclue de bogues (ne vous trompez pas dans l’appel de l’éxecutable), mais elle fait son boulot.
Exemple d’utilisation :
-2.31469 -2.25864
1.33762 -1.46862
-1.02542 3.69526
1.30239 5.09662
0.371384 0.955313
2.39291 2.18598
6.12848 -2.79489
-0.0602905 -0.43505
3.28993 -0.711843
3.8893 1.6782
Voir aussi ces quelques passages sur Wikipédia :
Simulation d’une loi normale et multi-normale
factorisation de Cholesky
Le code présenté ici est à jour et maintenu sur le projet Open Metaheuristics, dans le fichier random.hpp.
Téléchargements
Archive contenant le code C++ complet
: L’archive comprend le fichier C++, un exécutable pour Linux et la licence GPL.
(Zip - 23.9 ko)